The Origins of Ray Tracing in Computer Graphics

Although the concept of ray tracing predates its use in computer graphics, the 1979 paper from Turner Whitted on An Improved Illumination Model for Shaded Display¹ is generally acclaimed to be the origins of modern ray tracing. Following his work, Cook et al. extended the concept to additional visual effects with Distributed Ray Tracing². The ray tracing approach was then summarized into The Rendering Equation³ by James T. Kajiya, who also introduced the concept of path tracing.

An Improved Illumination Model for Shaded Display

At the time of this paper from Whitted, shading models were much more simple. For example, the simplest form of Lambertian shading is based only on the cosine law that states the amount of light that a surface receives is directly proportional to the angle between the surface normal ($\hat{n}$$\hat{n}$) and the light direction ($\hat{L}$$\hat{L}$). A slightly more sophisticated model was the Phong model, which also considered reflections of ambient light and specular reflections.

The two gaps of previous works that Whitted highlights are:

1. These shading models do not account for objects within a scene acting as light sources or for light reflected from object to object.
2. Previous ray tracing algorithms end when the nearest intersection of a ray with objects in the scene is found and do not produce further rays.

The improved model that Whitted proposes is summarized as:

The light intensity, $I$$I$, passed to the viewer from a point on the surface consists primarily of the specular reflection, $S$$S$, and transmission, $T$$T$, components. These intensities represent light propagated along the $\overline{V}$$\bar{V}$, $\overline{R}$$\bar{R}$, and $\overline{P}$$\bar{P}$ directions, respectively.

Global Illumination

Whitted explains global illumination as a tree of light rays that accumulate to the light intensity at the point of interest.

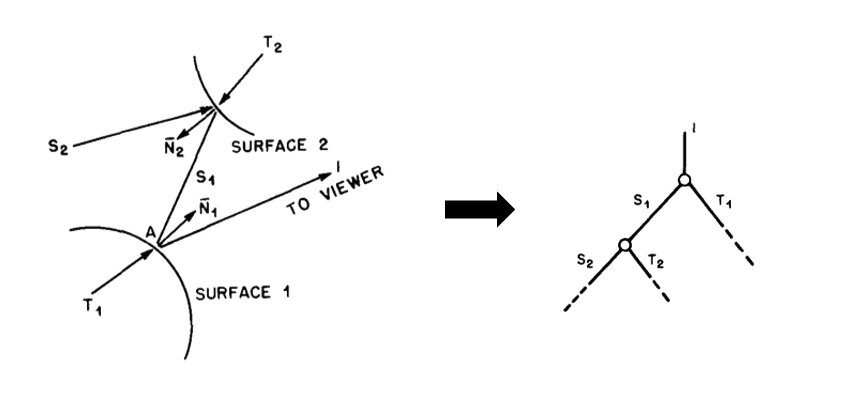
A visible surface algorithm that defines ray tracing is executed recursively until all the branches of this ray tree are terminated. For each ray, intersection tests are computed against bounding spheres in the scene. On hit, bounding spheres are subdivded with Catmull-Clark subdivision, bounded into a new, smaller sphere, and intersected again. This continues until there is a miss or the size of the bounding sphere is smaller than a predetermined threshold. This traversal algorithm shapes the traversal and intersection units of modern ray tracing hardware.

Some additional considerations are made for anti-aliasing by recursively subdividing the pixel sample square until rays from all four corners of the square generate similar intensity values. Bounding spheres are also restricted to a minimum size to prevent small objects from being lost.

Distributed Ray Tracing

Cook et al. expanded upon the idea of ray tracing and introduced more visual effects that can be generated beyond the global illumination described by Whitted. Some of these effects are:

• Blurred reflections
• Blurred transparency
• Soft shadows with penumbras
• Depth of field
• Motion blur

Each of these effects are generated by sampling rays in a different dimension. For each bounce in the Whitted algorithm, rays are only generated in the $\overline{R}$$\bar{R}$, $\overline{P}$$\bar{P}$, and the direction of the light sources in a distinct, point-sampling approach. However, scattering effects are generally more complex and bounce in a range of possible directions.

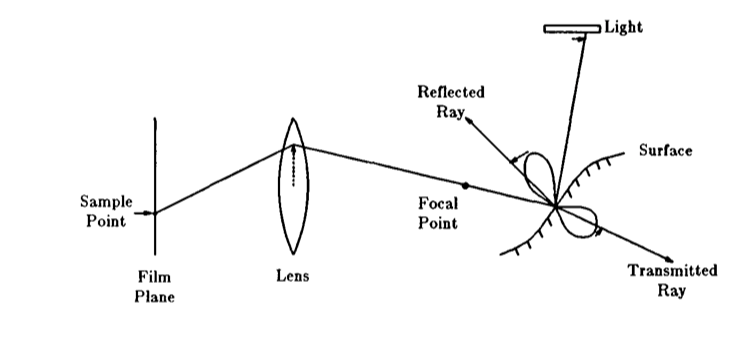
Instead, Cook et al. propose to sample simultaneously in multiple dimensions and distribute the existing ray budget into generating all of the above effects at once. Each visual effect should not be considered isolated problems because all of these phenomena are related and contribute together to image synthesis. Thus, for each sample point, the ray generated should consider the camera lens which creates the focal point, the reflectance and transmittance distributions, area light sources, and the concept of time.

The Rendering Equation

The ideas of ray tracing were summarized into the physically-based rendering equation in 1986. The equation balances the energy flow from one point of a surface to another with the law of conservation of energy by enclosing all energy inside a global background surface of $S_o$$S_o$. The equation states that:

The transport intensity of light from one surface point to another is simply the sum of the emitted light and the total light intensity which is scattered toward $x$$x$ from all other surface points.

Unoccluded Multipoint Transport

Each term in this equation describe the transport of radiance and can be converted to more conventional quantities by considering the geometric properties of the surfaces with angles.

• $I(x,x^{\prime })$$I(x, x’)$ is the unoccluded two point transport intensity which represents the energy of radiation per unit time per unit area of source per unit area of target.
• $g(x,x^{\prime })$$g(x, x’)$ is the geometry term which encodes occlusion and also $\frac{1}{r^2}$$\frac{1}{r^2}$ attenuation. 💡 This term is the result of the ray tracing query.
• $ϵ(x,x^{\prime })$$\epsilon (x, x’)$ is the emittance term or the unoccluded two point transport emittance, which represents the energy emitted by a surface per unit time per unit area of source per unit area of target.
• $\rho (x,x^{\prime },x^{″})$$\rho (x, x’, x’’)$ is the scattering term or the unoccluded three point transport reflectance, which represents the intensity of energy scattered by $x^{\prime }$$x’$ originating from $x^{″}$$x’’$.
• $I(x^{\prime },x^{″})$$I(x',x'')$ recursively models the energy of radiation per unit time per unit area of source per unit area of target of the energy scattered at $x^{\prime }$$x'$

Path Tracing

The other notable contribution from this paper is the concept of path tracing. Path tracing is defined here as a faster form of ray tracing that effectively prunes the tree of rays described by Whitted. It is based on the insight that the first generation of rays are the most important contributers to the integral and later generation rays contribute progressively less to the final result. In the original Whitted paper, rays are recursively generated at each bounce, which leads to a heavy distribution of rays at later bounces where the impact per ray is much lower. Kajiya proposes instead to shoot a path with the rays chosen probabilistically rather than shooting a branching tree.

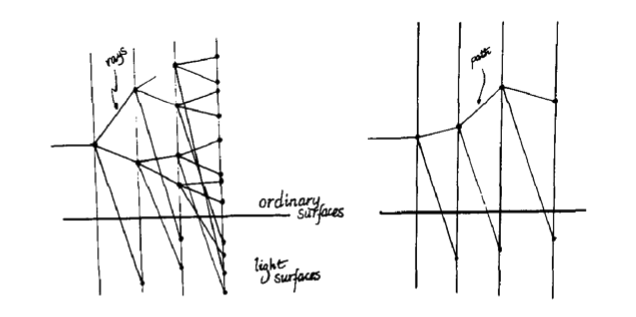
However, by limiting ray generation to a single ray per bounce, careful consideration must be made to the choice in the type of rays to shoot. Kajiya offers the method of tracking the number of each type shot and aiming to match the sample distribution of ray types closely to the desired distribution by varying the probability of each type.

Conclusion

Whitted, Cook et al., and Kajiya formed the foundations of modern ray tracing. Modern designs are built upon the traversal and intersection algorithm described by Whitted, model the visual effects outlined by Cook et al., and sample rays in the path tracing style of Kajiya. Global illumination techniques today still follow the rendering equation, and sophisticated sampling approaches still target the same light integral. An updated form of the rendering equation describes the light transport in terms of $\omega$$\omega$ directions instead.